What Happens After the Model?

Max Kuhn, Ph.D. (Posit, PBC)

Introduction

Thanks for staying until the last talk of the conference 😄


My goal is to stimulate our thoughts on supporting models once they are deployed.


Most of this talk is informed by my experiences in early drug discovery as well as developing algorithms for instrumented diagnostics (infection diseases).


Let’s start with an example.

Some example data

Computational chemistry QSAR data were simulated for a numeric outcome:

  • n = 6,000 training set.
  • n = 2,000 test set.
  • n = 2,000 validation set.
  • 20 molecular descriptors (unrealistically small)

Let’s suppose it is an assay to measure blood-brain-barrier penetration.

Model Development

A few models were tuned:

  • boosted trees (lightgbm)
  • Cubist rules
  • nearest-neighbor regression
  • neural networks (single layer, FF)

Several preprocessors were also assessed: nothing, partial least squares, and the spatial sign.

Each was tuned over their main parameters using 50 candidates.


The validation set RMSE was used to choose within- and between-models.

Model Selection

We ended up using one of the numerically best models: a neural network

  • 9 hidden units with tanh activation
  • weight decay of \(10^{-9.1}\)
  • a learning rate of \(10^{-1.5}\), trained over 221 epochs

Performance statistics (RMSE)

  • validation set: 0.254
  • test set: 0.258

Calibration

It’s pretty easy to just look at the metrics (RMSE) and make decisions.

The only way to be comfortable with your data is to never look at them.


For any type of model, we should check the calibration of the results. Are they consistent with what we see in nature?

  • Classification: we try to see if our probability estimates match the rate of the event.

  • Regression: we plot observed vs predicted values.

Calibration Results

Calibration

Some models (like ensembles) tend to under-predict at the tails of the outcome distribution.

If that’s the case, our best avenue is to try a different model.

Otherwise, we can try to estimate the calibration trend and factor it out.

Data usage and validation can be tricky with this approach but it can work well.

What’s Next?

Let’s assume that we will enable others to get predictions from our model.

In our example, we would deploy our model so that medicinal chemists would predict specific compounds or make predictions en masse.


We have consumers of our models now.

What other activities should we pursue to ensure that the model is used effectively and safely?

  • Documentation
  • Characterization
  • Monitoring

Documentation

How was the model created?

  • Methodology
  • Data
    • numbers
    • scope (local or global?)
    • limitations
    • provenance
  • Efficacy claims (“our test set RMSE was
”)

How does the model function?

  • Mathematically
  • What are the main ingredients?
  • Where is it applicable? WCGW?
  • How shall I explain predictions?
  • Is it fair?

etc.

Characterization

How Does it Work?

There is a whole field of literature on model explainers.

These can be categorized into two groups: global and local explainers.

  • Global methods characterize the model.

  • Local explainers elucidate predictions.

We’ll look at two global methods.

Importance Scores

Variable importance scores are used to quantify the overall effect of a predictor on the model.

There are model-specific methods to compute importance for some models.

More broadly a permutation approach can be used to eliminate the predictors’ effect on the model and see how performance changes.

Partial Dependence Plots

For important features, we can also understand the average relationship between a predictor and the outcome.

Partial dependence plots and similar tools can help consumers understand (generally) why a predictor matters.

Prediction Intervals

For end-users, a measure of uncertainty in predictions can be very helpful.

An X% prediction interval is a bound where the next observed value is within the bound X% of the time.


Most ML models cannot easily make these but two tools that can work for any regression model are:

  • Bootstrap intervals (expensive but solid theory)
  • Conformal inference (fast but still evolving)

90% Prediction Intervals

Monitoring

Tracking Performance

If we deploy a model, especially with an internal/public API, we should check to see how it does over time.


Assuming that we get labeled data within some unit of time, we should report performance (preferably to the customers).


Let’s look at the first 10 post-deployment weeks where about 40 molecules are available each week.

Post- Deployment Monitoring

Drift

We often hear about model drift but there is no such thing.


Data drift may change over time and that can affect how well our model works if we end up extrapolating outside of our training set.

There is also concept drift: the model starts being used for some other purpose or with some other population.


The assay simulated here was designed to

  • measure whether compounds crossed the blood-brain-barrier

  • mostly to verify that they do not get into the brain.

Maybe we should look into this


Data Drift or Concept Drift?

Smaller molecules

Define the Applicability Domain

Prior to releasing a model, document what it is intended to do and for what population.

  • This is called the model’s applicability domain.


We can treat the training set as a multivariate reference distribution and try to measure how much (if at all) new samples extrapolate beyond it.

  • Hat values
  • Principal component analysis
  • Isolation forests, etc.

PCA for Applicability Domain

PCA Reference Distirbution

Quantifying Extrapolation

Isolation Forests

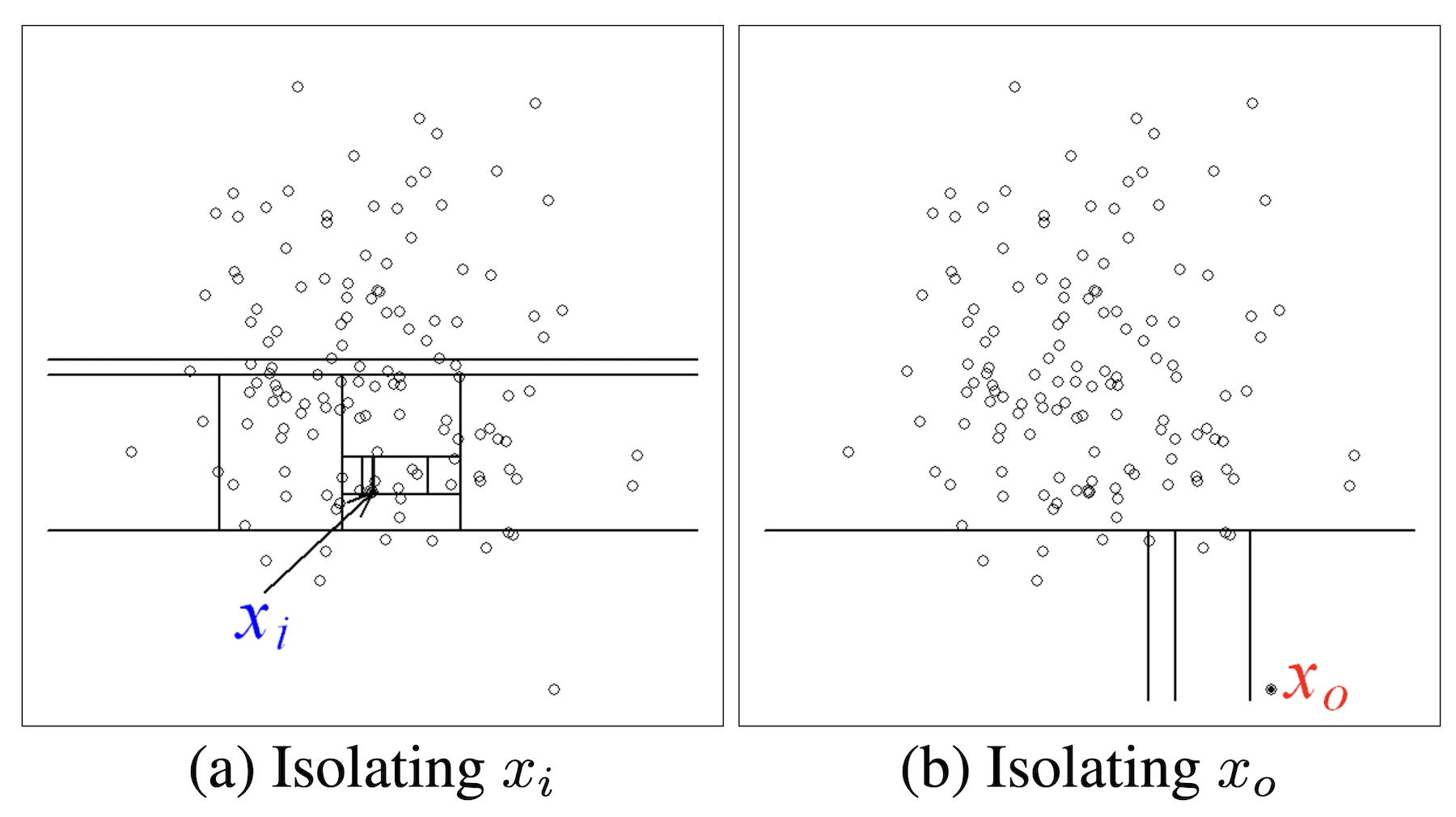
(from Liu, Ting, and Zhou (2008))

Monitoring via Isolation Forests

Scoring New Data

Using any of the applicability domain methods, we can add a second unsupervised score to go along with each individual prediction:

Your assay value was predicted to be 6.28, indicating that the molecule signficantly crosses the blood-brain barrier.

However, the prediction is an extraploation that is very different from the data that was used to create the model (score: 0.97). Use this prediction with extreme caution!

Thanks

Thanks for the invitation to speak today!


The tidymodels team: Hannah Frick, Emil Hvitfeldt, and Simon Couch.


Special thanks to the other folks who contributed so much to tidymodels: Davis Vaughan, Julia Silge, Edgar Ruiz, Alison Hill, Desirée De Leon, Marly Gotti, our previous interns, and the tidyverse team.

References (1/2)

Model fairness:

Conformal Inference

References (2/2)

Applicability Domains:

Explainers:

https://topepo.github.io/2024_PharmaDS