1  Introduction

Machine learning (ML) models are mathematical equations that take inputs, called predictors, and try to estimate some future output value. The output, often called an outcome or target, can be numbers, categories, or other types of values.

For example, in the next chapter, we try to predict how long it takes to deliver food ordered from a restaurant. The outcome is the time from the initial order (in minutes). There are multiple predictors, including: the distance from the restaurant to the delivery location, the date/time of the order, and which items were included in the order. These data are tabular; they can be arranged in a table-like way (such as a spreadsheet or database table) where variables are arranged in columns and individual data points (i.e., instances of food orders) in rows, as shown in Table 1.21.

Note that the predictor values are almost always known. For future data, the outcome is not; it is a machine learning model’s job to predict unknown outcome values.

TODO: In Figure 1.1, we get a “(a)” between the image and the caption.

(a)
(b)
Figure 1.1: Histrograms of the training set outcome data with and without a transformation.

TODO The next figure, , is included images and another “(a)” and produces a warning in the terminal:

(a)
(b)
Figure 1.2: A general high level view of the process of creating a predictive model. The diagram reflects which steps use the test set, validation set, or the entire training set.

TODO We should think about about doing more than a warning when a traditional chunk is used in a book with renderings: [light, dark] and without fenced chunks.

Here’s an example that appears to work but when you switch to dark mode, the figure number changes.

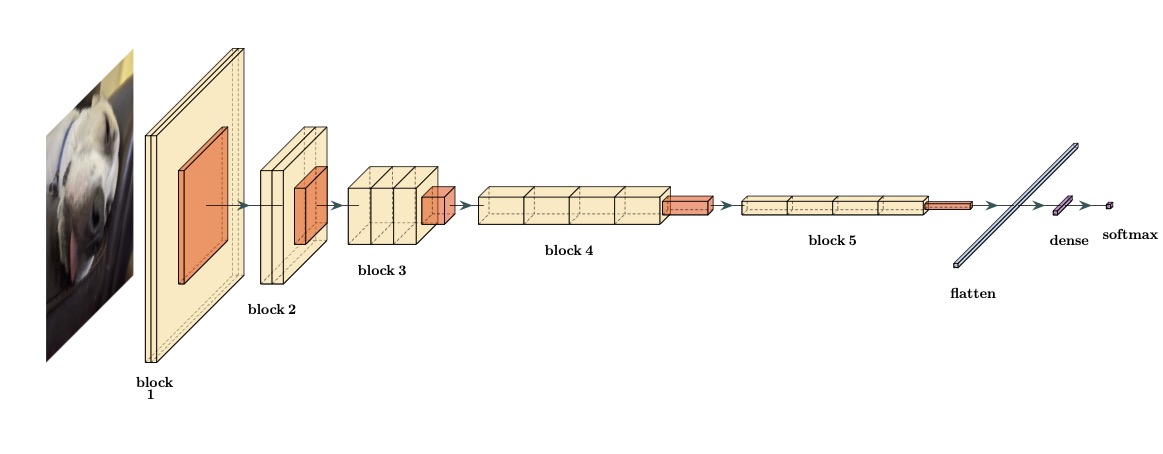
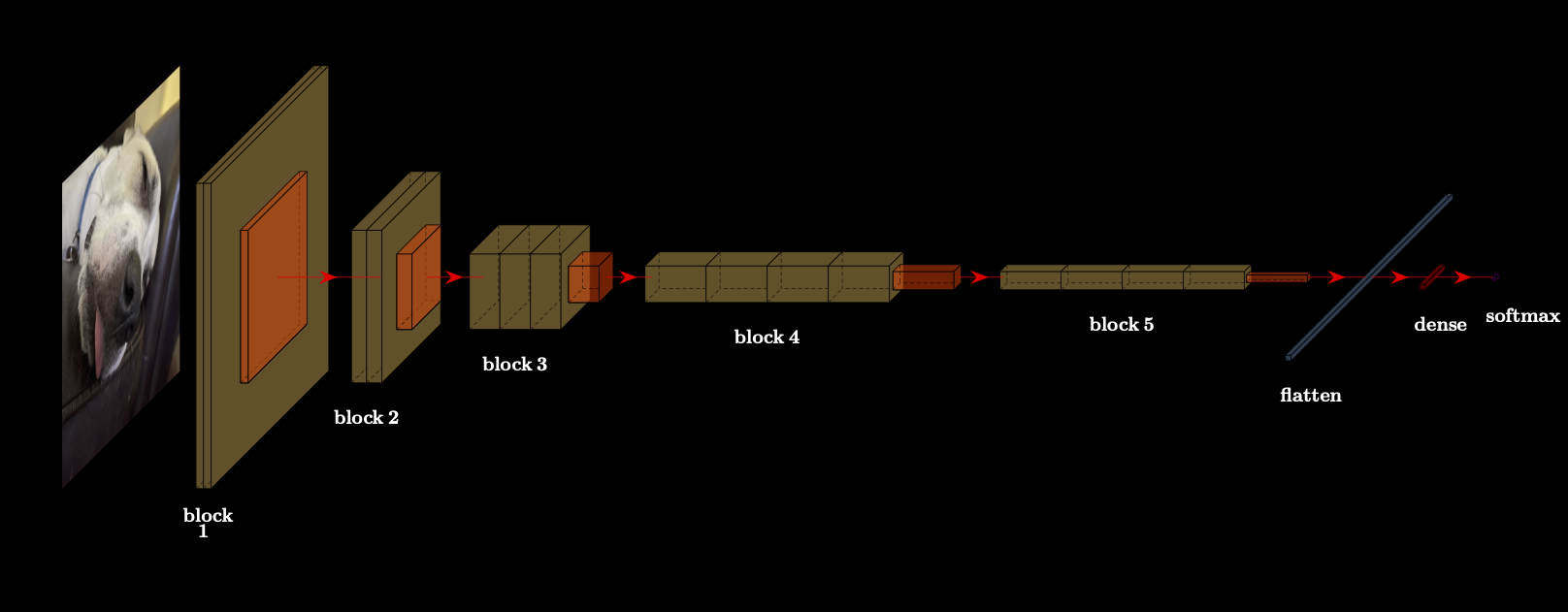
Figure 1.3: A simplified version of the convolutional neural network deep learning model proposed by Simonyan and Zisserman (2014). This version only includes a single dense layer (instead of four).
Figure 1.4: A simplified version of the convolutional neural network deep learning model proposed by Simonyan and Zisserman (2014). This version only includes a single dense layer (instead of four).

1.1 A Table

TODO A few issues with Table 1.1 below:

  • Another “(a)”
  • Both tables show up
  • gt_theme_dark() capitalizes columns ¯\(ツ)/¯
  • Also, why are figure captions left aligned but tables are right aligned.
ID Eccentricity Area Intensity
Nucleus Cell Nucleus Cell Nucleus Cell
17 0.494 0.836 3,352 11,699 0.274 0.155
18 0.708 0.550 1,777 4,980 0.278 0.210
21 0.495 0.802 1,274 3,081 0.326 0.218
22 0.809 0.975 1,169 3,933 0.583 0.229
ID Eccentricity Area Intensity
Nucleus Cell Nucleus Cell Nucleus Cell
17 0.494 0.836 3,352 11,699 0.274 0.155
18 0.708 0.550 1,777 4,980 0.278 0.210
21 0.495 0.802 1,274 3,081 0.326 0.218
22 0.809 0.975 1,169 3,933 0.583 0.229
(a)
Table 1.1: Cells, such as those found in a previous figure, translated into a tabular format using three features for the nuclear and non-nuclear regions of the segmented cells.

I just put the next table to see if we get the reference number changing when you go between light/dark (it did not for me).

Time to Delivery Hour of Order Day of Order Distance Item Counts
1 2 ... 27
15.26 11.9 Thu 2.82 0 0 ... 0
27.45 19.2 Wed 3.59 0 0 ... 1
25.50 14.9 Thu 2.28 2 0 ... 0
17.34 12.2 Wed 3.26 0 0 ... 0
13.58 11.5 Fri 2.15 2 0 ... 0
25.55 15.4 Sat 2.17 0 0 ... 0
19.86 13.2 Tue 2.67 0 0 ... 0
28.25 15.7 Sun 4.24 1 0 ... 1
Time to Delivery Hour of Order Day of Order Distance Item Counts
1 2 ... 27
15.26 11.9 Thu 2.82 0 0 ... 0
27.45 19.2 Wed 3.59 0 0 ... 1
25.50 14.9 Thu 2.28 2 0 ... 0
17.34 12.2 Wed 3.26 0 0 ... 0
13.58 11.5 Fri 2.15 2 0 ... 0
25.55 15.4 Sat 2.17 0 0 ... 0
19.86 13.2 Tue 2.67 0 0 ... 0
28.25 15.7 Sun 4.24 1 0 ... 1
Table 1.2: A random selection of several rows from a tabular data set on food delivery times.

Chapter References

Simonyan, K, and A Zisserman. 2014. “Very Deep Convolutional Networks for Large-Scale Image Recognition.” arXiv.

  1. Non-tabular data are later in this chapter.↩︎